Anomalous surface currents in the tropical Indian Ocean
Submitted
to the Geophysical Research Letters.
June 28, 2001
Revised:August
26, 2001
<<Please use the NETSCAPE browser>>
Abstract
An anomalous climate event occurred in 1997 in
the Indian Ocean with severe consequences for the surrounding continental
areas. In response to an intensification of the trade winds, a westward
gradient of SST and an anomalous reversal of the eastward surface currents
with peak velocity anomalies exceeding 1 m/s were evident in the boreal
autumn. A similar but weaker event took place in 1994. In this study we
examine the observational record during the 1990s including surface drifter
velocities, SST and altimeter sea level to confirm these dramatic changes.
We examine the key momentum balance between wind-induced momentum flux
and the pressure gradient force as well as the important role of horizontal
temperature advection in the mixed layer heat response.
1.
Introduction
During
boreal autumn of 1997 the meteorological conditions in the tropical Indian
Ocean were quite unusual. The trade winds extended equatorward and intensified
by 0.3 dyn/cm2. The zonal component of wind stress on the equator
(normally eastward and weak this time of the year) reversed direction and
increased by 0.1 - 0.2 dyn/cm2 as well. In response the eastern
basin SST cooled by 10C to 30C along and south of
the equator with a corresponding drop in sea level, while in the western
basin there was substantial warming of SST albeit with a phase lag [Yu
and Reinecker, 1999; Potemra and Lukas, 1999; Saji
et al., 1999; Webster et al., 1999; Murtuggude et al.,
2000; Susanto et al., 2001]. Recent modeling studies suggest the
importance of horizontal advection within the mixed layer acting directly
on the zonal gradient of mixed layer temperature in inducing a dipole SST
pattern, and indirectly in forcing an east-west gradient in thermocline
depth by redistributing mass [Murtugudde et al., 2000]. Here we
exploit the availability of direct observations of near-surface velocity
to document these remarkable changes in the context of a 9-year record
and examine the role of advection in thermodynamics along the equator.
Much
of our empirical knowledge of the seasonal changes in the Indian Ocean
surface currents comes from analyses of historical shipdrift observations
[Cuttler and Swallow, 1984; Rao et al., 1989] and near surface
drifter tracks [Molinari et al., 1990]. The annual mean surface
currents on the equator are eastward. Their seasonal variation has a well-pronounced
semi-annual harmonic. During the boreal winter (JFM), the currents are
dominated by the westward North Equatorial Current with speeds of 50 cm/s
extending from 900 E to Africa. During spring (AMJ) and late
autumn (OND), the eastward equatorial jet develops peaking at about 1 m/s
in autumn [Wyrtki, 1973]. In the summer (JAS), a weak westward flow
is observed in the west. Superimposed on this seasonal variability are
interannual fluctuations closely linked to ENSO [see e.g. Cadet,
1985]. However, detailing these changes has been difficult in the absence
of direct observations. Fortunately, extensive deployments of the 15m-drogued
drifters were carried out as a part of the WOCE Global Data Surface Velocity
Programme [Niiler et al., 1987; Hansen and Poulain,
1996]. In this study we combine the drifter observations and the altimeter
sea levels using a multivariate optimal interpolation algorithm to produce
monthly mean surface currents in the Indian Ocean on a regular 30
x 20 grid. The resulting current analysis shows stunning changes
in momentum and mass during the 1997-8 event and also reveals the coincidence
of the Indian Ocean near-surface currents and the Pacific winds throughout
the decade.
2.
Data and analysis
This
study is based on five data sets; altimeter sea level, 15m-drogued drifter
velocity, climatological surface velocity estimates from historical shipdrift,
Sea Surface Temperature (SST) data, and NCEP/NCAR reanalysis winds. The
TOPEX/POSEIDON altimeter sea level is obtained from the Pathfinder version
2.1 archive [Koblinsky, personal communication, 1997]. This data
spans the interval from late September 1992 through the end of our analysis
period, October 2000, with a 9.92-day repeat cycle and a near-equatorial
track spacing of 2.80. After the usual corrections for geophysical
effects, the sea level estimates have been averaged into 10
latitude segments.
Surface
drifter currents are obtained from the WOCE/TOGA archive at the Atlantic
Ocean Marine Laboratory (NOAA/AOML). The data spans the period February
1979 - October 2000. The drifter tracks are converted to six-hourly velocity
estimates as described by Hansen and Poulain [1996]. These
currents are averaged into 20x30x1-month bins, which
then form the basic data set for our study.
To
provide a first guess for our analysis we also use ship-drift velocity
estimates available on the Ocean Current Drifter Data CD-ROM provided by
NOAA/NODC to construct a climatological monthly cycle of currents. The
results of this preliminary analysis are very comparable with the climatology
of Cutler and Swallow [1984], as described below. Our analysis includes
ageostrophic effects estimated based on NCEP/NCAR reanalysis surface wind
stress [Kalnay et al., 1996]. To evaluate the heat balance we use
the SST provided by the analysis of Reynolds and Smith [1994].
Finally, we use independent 20-30m velocity estimates from shipboard Acoustic
Doppler Current Profilers acquired from the Joint Archive for Shipboard
ADCP at University of Hawaii to provide an independent estimate of velocity
error.
The
procedure for mapping surface currents follows the methodology of multivariate
statistical interpolation [Daley, 1991; Grodsky and Carton,
2001]. Near surface velocity can be decomposed into a geostrophic component
and winddrift. Following Lagerloef et al. [1999], we assume that
the winddrift satisfies an Ekman-like equation balancing the difference
between the wind-induced momentum flux and the linear friction with the
Coriolis force. A simple linear friction term is included to allow an Ekman-like
balance to account for the ageostrophic component on the equator. The geostrophic
component of the mixed layer analysis velocity, ![]() ,
is then written as a linear combination of the weighted differences between
the observations, 'O', and the background estimates, 'B',
of sea level,
,
is then written as a linear combination of the weighted differences between
the observations, 'O', and the background estimates, 'B',
of sea level, ![]() ,
and the mixed layer velocity, u,
,
and the mixed layer velocity, u,
3.
Results
During
the boreal fall the eastward Wyrtki jet and an eastward Indian Monsoon
Current located slightly north of the equator develop in response to the
summer monsoon winds [Wyrtki, 1973] (see Figure 1). South
of the equator the South Equatorial Current (SEC) flows westward along
100 S in the eastern basin and shifts to 150 S west
of 800 E. The contrast to conditions in 1997 is striking. During
the fall of that year the surface currents on the equator became westward
in response to a strengthening of the trade winds with anomalies exceeding
1 m/s and a significant meridional divergence. The SEC intensified also
in the east while weakening in the west. The strongest equatorial divergence
probably exists close to the coast of Sumatra where the anomalous flow
is poleward on both sides of the equator and divergence exceeds 4*10-7
s-1 (see Figure 1).
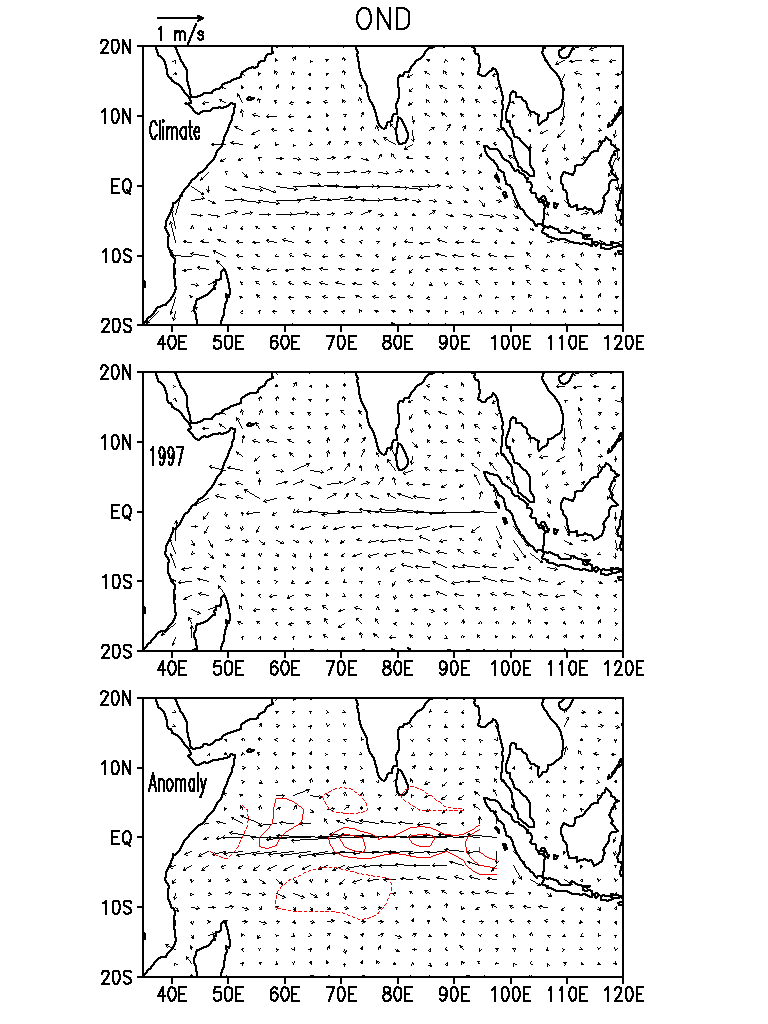 |
|
Figure
1.
October-November-December average currents in the Indian Ocean: (top) climatology,
(middle) year 1997, and (bottom) 1997 anomaly from climatological mean.
Contours show anomalous current divergence at [-1, 1, 2, 4, 8]*10-7
1/s levels. Negative isolines are shown with dashed lines.
|
The
development of the westward equatorial jet is clearly related to changes
in the winds in the Indian Ocean sector. In the Pacific Ocean Yu
and McPhaden [1999] found the near surface equatorial zonal momentum
to be dominated by a three-term linear balance between local acceleration, ![]() ,
zonal pressure gradient,
,
zonal pressure gradient, ![]() ,
and zonal wind stress,
,
and zonal wind stress, ![]() ,
the first three terms of (2)
,
the first three terms of (2)
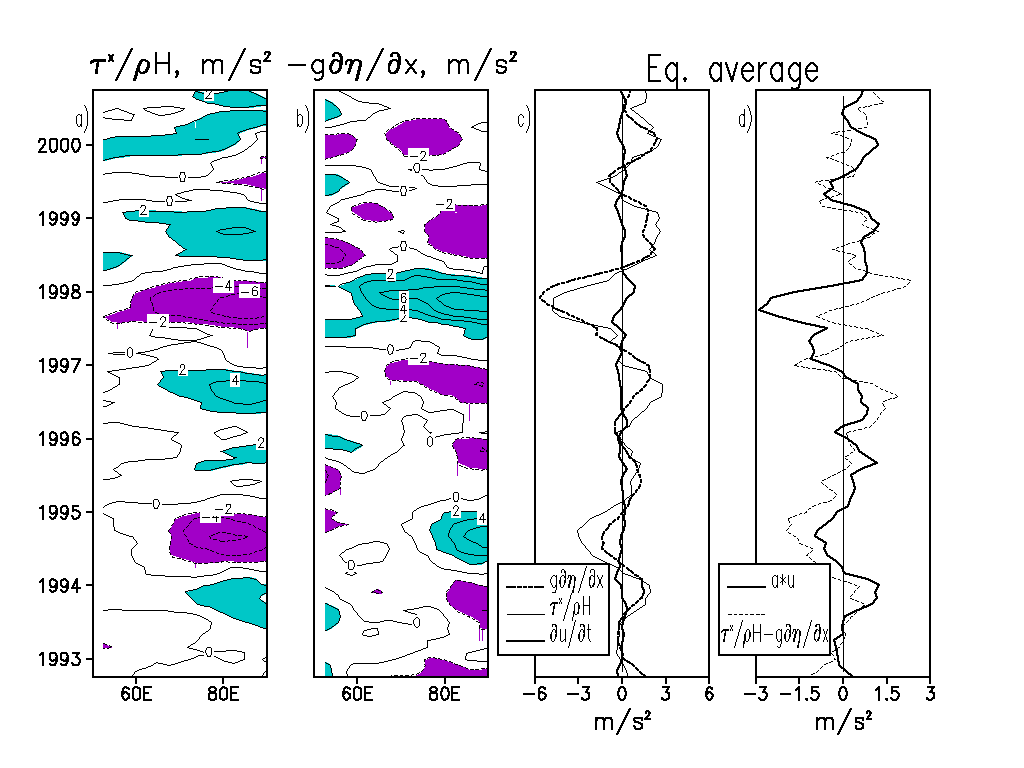 |
|
Figure
2.
Time-longitude equatorial diagrams of (a) anomalous wind stress force and
(b) pressure gradient force. Panel (c) shows zonal averages of the terms
presented in (a, b) along with anomalous local acceleration. Panel (d)
compares Rayleigh friction with the sum of the other terms. All values
are multiplied by 107.
|
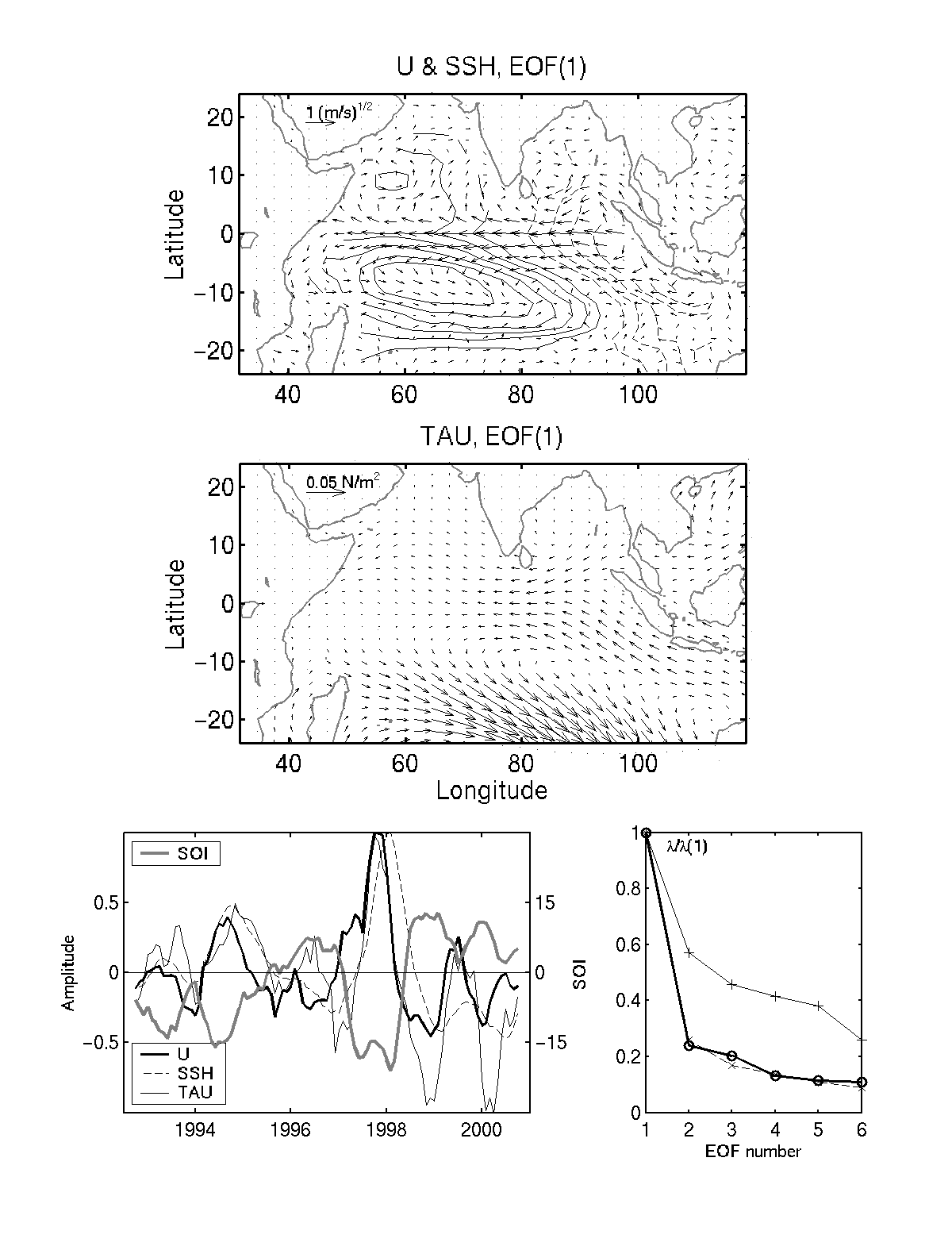 |
|
Figure
3.
Leading interannual EOFs of surface velocity (U), sea level (SSH), and
wind stress (TAU). The principal component time series along with the Southern
Oscillation Index and relative sizes of eigenvalues are shown in the bottom
line. Sea level contour intervals - 3 cm. Negative isolines are shown with
dashed lines. Surface current arrows are of the vector field
|
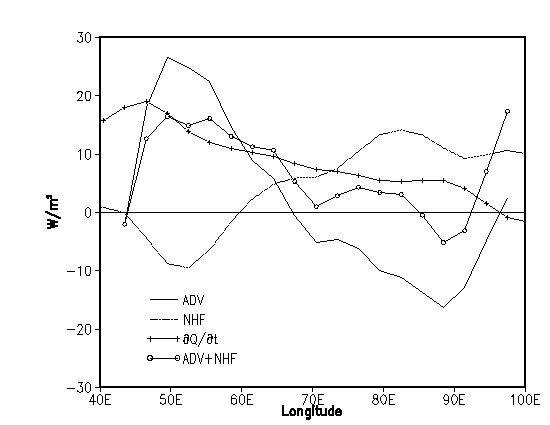 |
|
Figure
4. Terms
in the anomalous heat budget along the equator, annually averaged for 1997.
Terms include -
rate of change of heat content,
|
The 1993-2000
period covers two anomalous easterly wind events one during 1994 and the
other during 1997. The 1994 event has been described by Vinayachandaran
et al. [1999] who found a persistent easterly wind anomaly in the east
(east of 700 E) beginning in April and lasting for at least
8 months. The 1997 event was stronger and observed well west of 600
E (see Figure 2a). As a result, the 1994 and 1997 events had quite
similar cooling in the east, but there was no warming in the west in 1994
[Murtugudde et al., 2000].
The strengthening of the easterly wind also prevents the development of the Wyrtki Jet, which appears during the transition periods between the monsoons. In contrast the fall transition period (OND) currents on the equator in 1997 were westward (see Figure 1). A similar but a weaker event took place in the second half of 1994. Our analysis for that year shows that the westward current anomaly was ~0.3 - 0.4 m/s, so that the Wyrtki jet developed but was weaker than the climatological one.
Both, the 1994 and 1997 events coincide in time with the ENSO events in the Pacific Ocean. Moreover, Potemra and Lukas [1999], Susanto et al. [2001], Murtugudde [private communication] as well as our analysis show that eastern equatorial Indian Ocean dynamics is intimately related to ENSO forcing at least during the decade of 1990s. Although longer time records demonstrate that a unique and inherent air-sea dynamics over the Indian Ocean contributes significantly [Vinayachandaran et al., 1999].
Acknowledgments
SG and JC gratefully acknowledge support from the National Science Foundation (OCE9812404) to JAC. RM would like to acknowledge NASA salinity and Indian Ocean grants. We are grateful to the Drifter DAC of the GOOS Center at NOAA/AOML for providing the drifter data set.
References
Cadet, D. L., The Southern oscillation over the Indian Ocean, J. Climatol., 5, 189-212, 1985.
Carton, J. A., G. Chepurin, X. Cao, and B. Giese, A simple Ocean Data Assimilation analysis of the global upper ocean 1959-1995, Part 1: Methodology, J. Phys. Oceanogr., 30, 294-309, 2000.
Cutler, A. N., and J. C. Swallow, Surface currents in the Indian Ocean (to 25S, 100E). Rep. 187, 42 pp., Inst. of Oceanogr. Sci., Wormley, England, 1984.
Daley, R., Atmospheric Data Analysis, Cambridge University Press, 457 pp., 1991.
Grodsky, S. A., and J. A. Carton. Intense surface currents in the Tropical Pacific during 1996-1998, J. Geoph. Res., 106, 16,673-16,684, 2001.
Hansen, D. V., and P.-M. Poulain, Quality control and interpolations of WOCE-TOGA drifter data, J. Atmos. Oceanic Technol., 13, 900-909, 1996.
Kalnay, E., and Coauthors, The NCEP/NCAR 40-year reanalysis project, Bull. Amer. Meteor. Soc., 77, 437-471, 1996.
Lagerloef, G .S. E., G.T. Mitchum, R. B. Lukas, and P. P. Niiler, Tropical Pacific near surface currents estimated from altimeter, wind, and drifter data, J. Geophys. Res., 104, 23,313-23,326, 1999.
Molinari, R. L., D. Olson, and G. Reverdin, Surface current distributions in the tropical Indian Ocean derived from compilations of surface buoy trajectories, J. Geoph. Res., 95, 7217-7238, 1990.
Murtugudde, R., J. P. McCreary Jr., and A. J. Basalacchi, Oceanic processes associated with anomalous events in the Indian Ocean with relevance to 1997-1998, J. Geophys. Res., 105, 3295-3306, 1999.
Niiler, P. P., R. E. Davis, and H. J. White, Water following characteristics of a mixed layer drifter, Deep Sea Res., Part A,34, 1867-1882, 1987.
Picaut, J., S. P. Hayes, and M. J. McPhaden, Use of geostrophic approximation to estimate time-varying zonal currents at the equator, J. Geophys. Res., 94, 3228-3236, 1989.
Potemra, J. T., and R. Lukas, Seasonal to interannual modes of sea level variability in the western Pacific and eastern Indian Oceans, Geoph. Res. Let., 26, 365-368, 1999.
Ralph, E. A., and P. P. Niiler, Wind-driven currents in the Tropical Pacific, J .Phys. Oceanogr., 29, 2121-2129, 1999.
Rao, R. R., R. L. Molinary, and J. F. Fiesta, Evolution of the climatology near-surface thermal structure of the Indian Ocean. 1. Description of mean monthly mixed layer depth, and sea surface temperature, surface current, and surface meteorological fields, J. Geophys. Res., 94, 10,801-10,815, 1989.
Reynolds, R. W., and T. M. Smith, Improved global sea surface temperature analyses using optimum interpolation, J. Clim., 7, 929-948, 1994.
Saji, N. H., B. N. Goswami, P. N. Vinayachandran, and T. Yamagata, A dipole mode in the tropical Indian Ocean, Nature, 401, 360-363, 1999.
Susanto, R. D., A. L. Gordon, and Q. Zheng, Upwelling along the coast of Java and Sumatra and its relation to ENSO, Geoph. Res. Let., 28, 8, 1599-1602, 2001.
Webster, P. J., A. M. Moore, J. P. Loschnigg, and R. R. Leben, Coupled ocean-temperature dynamics in the Indian Ocean during 1997-98, Nature, 401, 356-360, 1999.
Yu, L. A, and M. M. Rienecker, Mechnisms for the Indian Ocean warming during the 1997-98 El Nino, Geoph. Res. Lett., 26, 735-738, 1999.
Yu, X. R., and M. J. McPhaden, Dynamical analysis of seasonal and interannual variability in the equatorial Pacific, J. Geophys. Res., 29, 2350-2369, 1999.
Vinayachandaran, P.N., N.H. Saji, and T. Yamagata, Response of the Equatorial Indian Ocean to an unusual wind event during 1994, Geoph. Res. Let., 26, 1613-1616, 1999.
Wyrtki, K. Equatorial jet
in Indian Ocean, Science, 181, 264-266, 1973.