Department of Meteorology

Please use the NETSCAPE browser

PDF, DOC, and pictures

1. Introduction

The seasonal cycle of shortwave radiation at the top of the atmosphere is primarily semiannual in the tropics, with maxima in boreal spring and fall. On the other hand, variability in the tropical Atlantic ocean-atmosphere system is dominated by the annual harmonic. The difference reflects seasonal changes in the radiative properties of the atmosphere and the dynamics and thermodynamics of the ocean. In this study we use direct observations, primarily from recently deployed moorings of PIRATA (Pilot Research Array in the Tropical Atlantic) (Servain et al., 1998), to examine the causes of the seasonal cycle of SST in response to seasonally varying surface heating and winds. 

Net surface heat flux is a combination of latent and sensible heat loss, shortwave radiation absorption, and net longwave emission. Sensible heat loss is insignificant (less than 10 W m^-2) due to small air-sea temperature differences, while net emission of longwave radiation is a relatively constant ~ 50 W m^-2(da Silva et al., 1994). Seasonal variations in latent heat loss and downwelling surface shortwave radiation are more significant. Both are influenced by the latitudinal movement of the narrow band of clouds associated with the Intertropical Convergence Zone (ITCZ), and shortwave radiation is additionally influenced by changes in the solar zenith angle. In the northern tropics latent heat loss is lowest during boreal summer and fall, when winds are weak and relative humidity is high (> 85%). Latent heat loss rises during boreal winter and spring when the ITCZ is close to the equator, low-level humidity is lower, and the northeast trade winds are stronger. In the eastern equatorial zone latent heat loss has only weak seasonal variations, as low-level relative humidity and wind speed are fairly steady throughout the year (da Silva et al., 1994).

In contrast to the shortwave radiation at the top of the atmosphere, surface shortwave radiation has a significant annual harmonic at most locations. North of 5ºN surface solar radiation reaches a maximum in boreal spring, when the ITCZ is near its southernmost position and the solar zenith angle is high. Between the equator and 5ºN there is a strong semiannual component, with maxima in boreal spring and fall, while on the equator the annual harmonic is again significant with increasing amplitude toward the west reaching maximum in boreal fall. The reduced amplitude in the east is due to the appearance of reflective stratus clouds in boreal fall over the cool waters of the eastern basin (Klein and Hartmann, 1993; Philander et al., 1996).

Like the tropical atmosphere, the tropical ocean also has a strong annual harmonic. A westward shift of warm (> 27ºC) SST in the latitude band 5-15ºN occurs in boreal summer, along with the development of a tongue of cool 23°C SST along and just south of the equator east of 30°W. This shift occurs concurrently with the annual growth and eastward expansion of the Atlantic warm pool west of 50°W (Wang and Enfield, 2001). In the west, seasonal changes in SST are weak in the equatorial zone, while north of 8°N a strong annual harmonic appears with a maximum in boreal fall. South of the equator SST reaches its maximum in boreal spring with an annual harmonic that increases in amplitude eastward to up to 3°C near the African coast (Reynolds and Smith, 1994).

The surface wind field is dominated by the northeast trade winds to the north of the ITCZ and the southeast trade winds to the south, with weakened winds between (da Silva et al., 1994). To the east a monsoonal circulation develops in boreal summer causing the northeast trades to reverse direction. Zonal currents develop in response to these changing winds and resulting Ekman divergence. On and south of the equator the westward South Equatorial Current is strongest in boreal summer, with speeds of 55 cm s^-1 in the central basin (Richardson and Reverdin, 1987). Close to the latitude of the ITCZ (5-10°N) the eastward North Equatorial Countercurrent is strong during boreal summer and fall with speeds of 35 cm s^-1. Between these two major current systems, and on the northern edge of the cold tongue, lie the strong meridional fluctuations of tropical instability waves, which we anticipate are important in transporting heat into the cold tongue in the eastern and central basin (Weisberg and Weingartner, 1988). 

A number of observational (e.g., Wyrtki, 1981; Enfield, 1986; Hayes et al., 1991; Wang and McPhaden, 1999; Swenson and Hansen, 1999) and modeling (e.g., Koberle and Philander, 1994; Kessler et al., 1998) studies have addressed the causes of the seasonal cycle of SST in the eastern equatorial Pacific. Observational studies in particular have had difficulty closing the heat budget. Hayes et al. (1991) used mooring observations in the eastern equatorial Pacific, together with surface meteorology, to calculate contributions to the mixed layer heat budget during 1986-1988. They found discrepancies between their forcing and actual heat storage that in some cases exceeded 100 W m^-2 and attributed these discrepancies to errors in parameterizations of mixed layer depth, entrainment, and meridional eddy heat divergence.

Wang and McPhaden (1999) used a combination of 15 years of daily mooring observations and climatological surface meteorology to estimate terms in the equatorial Pacific mixed layer heat budget. They estimated a mean seasonal cycle and found significant contributions from net surface heat flux and horizontal advection. They found discrepancies of up to 120 W m^-2 in the east and attributed these differences to a combination of two missing terms: vertical entrainment and vertical diffusion. Consistent with these results, Swenson and Hansen (1999) used a combination of drifting buoys and vertical temperature profiles to investigate the heat budget of the cold tongue. They found that strong seasonal cycles of entrainment and horizontal advection account for a large fraction of seasonal SST variability. 

In the equatorial Atlantic, Hastenrath (1977) and Merle (1980) used climatologies of surface heat flux and heat storage to deduce that horizontal and vertical temperature advection are necessary to balance the annual mean net surface heat flux. Molinari et al. (1985) used atmospheric and oceanic measurements from the First Global Atmospheric Research Program?s (GARP) Global Experiment (FGGE) in 1979 to explicitly evaluate the effects of surface energy fluxes and zonal temperature advection on the seasonal cycle of mixed layer temperature. Their results revealed important contributions from zonal advection between 3 - 9ºN. They calculated the sum of vertical and meridional advection/diffusion as a residual and found this term to be important within 3º of the equator. Unfortunately, none of the above studies was able to explicitly calculate the effects of meridional advection or vertical entrainment/diffusion on the mixed layer heat balance.

Weingartner and Weisberg (1991a,b) examined the seasonal heat budget based on one year of observations from an equatorial mooring at 28ºW (midbasin). They concluded that upwelling creates the cold SST tongue in boreal spring, while SST increases in boreal summer as the result of tropical instability waves. In late summer and fall advection terms are small and compensating and diffusion at the base of the mixed layer balances net surface heat gain. In boreal winter SST increases in response to a net surface heat flux concentrated by the shallower mixed layer. 

Modeling studies have also stressed the importance of ocean dynamics in the equatorial Atlantic heat budget. Carton and Zhou (1997) concluded that zonal mass divergence causes cooling in the equatorial region east of 20ºW, while meridional Ekman divergence plays an important role in the west. Their results indicate that solar heating is most important south of 5ºS and north of 10ºN, while latent heat loss is dominant in the western basin between 8 - 12ºN. DeWitt and Schneider (1999) also found that advection plays a crucial role in the equatorial region, while the importance of latent heat loss increases toward the subtropics.

The studies mentioned above reveal that surface fluxes as well as horizontal and vertical temperature advection play a major role in shaping the seasonal cycle of SST in the equatorial Atlantic. However, the limited duration (~ 1 year) and spatial coverage of previous in situ observational programs has hindered efforts to quantify these contributions. In this study we use a variety of in situ and satellite measurements, with extended duration and spatial coverage, to explicitly calculate all contributions (with the exception of vertical turbulent diffusion) to the mixed layer heat balance to obtain a quantitative picture of the tropical Atlantic seasonal mixed layer heat balance.

2. Data and Methods

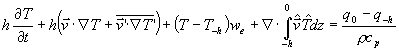.(1)

The terms represent, from left to right, local storage, horizontal advection (separated into mean and eddy terms), entrainment, vertical temperature/velocity covariance, and the combination of net atmospheric heating and vertical turbulent diffusion at the base of the mixed layer. Here h is the depth of the mixed layer, T and are temperature and velocity vertically averaged from the surface to a depth of -h, T? and are deviations from the time means (the overbar represents a time mean), and represent deviations from the vertical average, q₀ is net surface heat flux, while q_-h represents the sum of heat flux due to penetrative shortwave radiation and turbulent mixing at the base of the mixed layer. Swenson and Hansen (1999) estimate that the vertical temperature/velocity covariance term in (1) is less than 10% as large as other terms, and we therefore proceed to neglect this term. Entrainment velocity may be rewritten as , following Stevenson and Niiler (1983) (see their Eqs.(2) and (3)), and is associated with a mass flux that crosses an isopycnal surface.

Estimation of the terms in (1) requires knowledge of vertically averaged mixed layer horizontal velocity. Unfortunately, vertical profiles of velocity are not available at the PIRATA mooring locations. We therefore use alternative methods (described later in this section) to estimate mean and eddy advection terms in (1). 

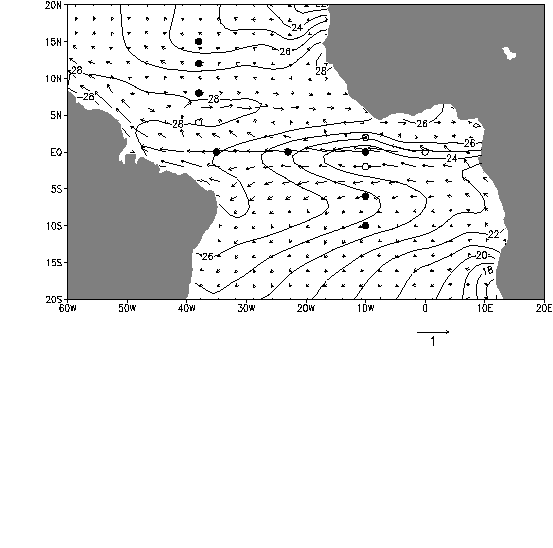
The PIRATA mooring array consists of 12 buoys (see Fig. 1). We focus on eight with record lengths exceeding two years. Deployed in 1997 to study ocean-atmosphere interactions, these Next Generation Autonomous Temperature Line Acquisition System (ATLAS) buoys measure subsurface temperature at 11 depths between 1 and 500 m with 20 m spacing in the upper 140 m. Air temperature and relative humidity are measured at a height of 3 m above sea level while shortwave radiation and wind velocity are measured at 3.5 and 4 m, respectively. The sampling interval is ten minutes for all variables except shortwave radiation, which is sampled at two-minute intervals. The instrument accuracies are: water temperature within ± 0.01ºC, wind speed ± 0.3 m s^-1 or 3% (whichever is greater), air temperature ± 0.2ºC, and relative humidity ± 3% (Freitag et al., 1994, 1999, 2001; Lake et al., 2002). Here we use both 10-minute and daily-averaged data, which are transmitted in near-real time via satellite by Service Argos. 
 
 

Fig. 1. Locations of the PIRATA moored buoys (solid and open circles). Solid circles indicate buoys with data records generally at least two years in length. Background contours and arrows are climatological July surface temperature (Reynolds and Smith, 1994) and near-surface velocity (Grodsky and Carton, 2001), respectively. Reference velocity arrow is 1 m s-1.

 

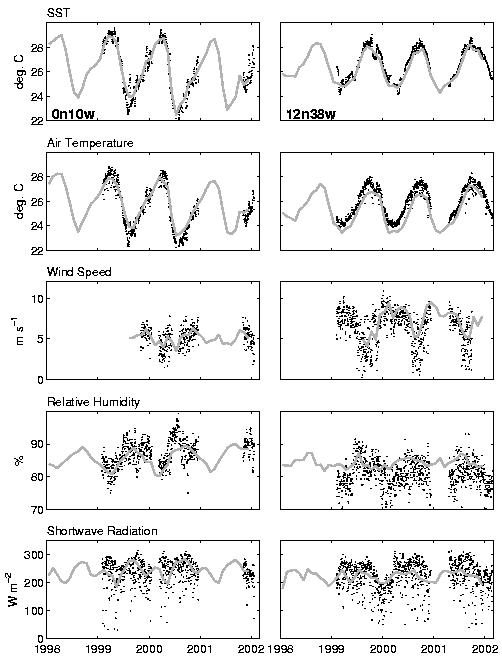
Fig. 2. PIRATA surface atmospheric and oceanic measurements at (left) 12°N, 38°W and (right) 0°N, 10°W during 1998-2002. Solid gray lines represent Reynolds and Smith (1994) SST, NCEP/NCAR Reanalysis (Kalnay et al., 1995) air temperature, relative humidity, and surface shortwave radiation (all at a height of 2 m), and Quikscat near-surface wind speed.

The amount of shortwave radiation absorbed in the mixed layer depends on the depth of the mixed layer and the optical transparency of the water. We have considered two models for penetrative shortwave radiation at the base of the mixed layer. One uses an empirical formula based on chlorophyll-a concentration, , where Q_surf is surface shortwave radiation, CHL is chlorophyll-a concentration (mg m^-3) from the Sea-viewing Wide Field-of-view Sensor (SeaWiFS), and h is the depth of the mixed layer (Morel, 1988). The second model follows Wang and McPhaden (1999) in assuming exponential decay of surface radiation with a constant 25 m e-folding depth. The seasonal cycle of penetrative solar radiation is strong at 12°N (Fig. 3) due to variations in mixed layer depth (varying from 21 m in October to 67 m in March, calculated according to the method described below in this section), but is weak along the equator at 10°W, where seasonal changes in mixed layer depth are relatively small (from 17 m in July to 34 m in October). Comparison of the two penetrative radiation models reveals that the chlorophyll-dependent equation always predicts more absorption. The bias is greatest along the equator at 10°W where chlorophyll concentration is high. However, since the bias is nearly constant throughout the year at all locations, both models result in similar seasonal cycles of absorbed solar radiation. For simplicity, and to avoid uncertainties inherent in the empirical formula, we will use the constant 25 m e-folding depth model to estimate penetrative radiation.
 
 

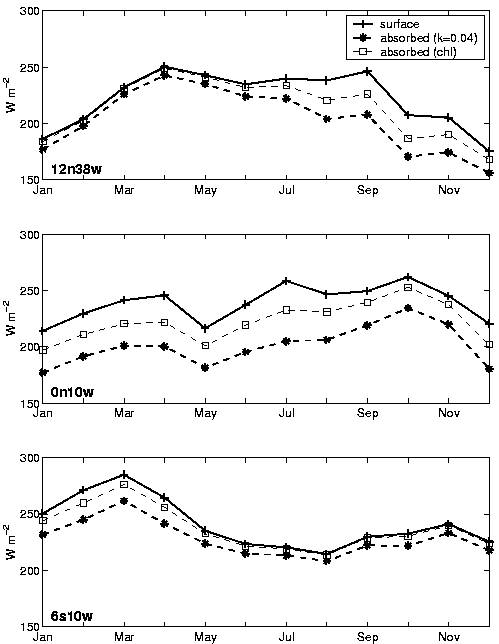Fig. 3. Climatological shortwave radiation at the surface and absorbed in the mixed layer, calculated with a constant e-folding depth of 25 m (k = 0.04) and a depth that depends on chlorophyll-a concentration (k=k(chl)), at three PIRATA locations.

 
 

Latent heat flux depends on surface humidity, wind speed, air temperature, and SST. Here we rely on a bulk parameterization, where Q_e is the latent heat flux, is air density, L_e is the latent heat of vaporization, is the transfer coefficient, W is wind speed,q is the water vapor mixing ratio, and is the interfacial water vapor mixing ratio, which is assumed to be proportional to the saturation water vapor mixing ratio (the factor of 0.98 accounts for salinity effects). Tests of this algorithm, developed from the Coupled Ocean-Atmosphere Response Experiment (COARE) in the tropical west Pacific (Fairall et al., 1996), have revealed a bias of 1.5 W m^-2 (COARE estimates lower) and a RMS scatter of less than 20% (Fairall et al., 1996). 

The COARE algorithm includes a model to estimate the effects of a diurnal warm layer and cool skin temperatures on latent heat flux. To determine the importance of these effects, we compared 10-minute latent heat flux estimates calculated without taking into account cool skin and warm layer effects to estimates that include both effects. We find that the cool skin effect dominates at all mooring locations, leading to a reduction in latent heat flux of 4-8 W m^-2 (mean bias over the length of each data record), with very little seasonal dependence. The effect is greatest at 8°N and 12°N along 38°W, where it can reduce latent heat flux by up to 10 W m^-2 on a monthly basis. The diurnal warm layer increases latent heat flux by less than 0.5 W m^-2 at all locations. Unfortunately, gaps in the PIRATA shortwave radiation records (solar radiation is required for calculation of both warm layer and cool skin effects) have led us to neglect both warm layer and cool skin effects in our analysis. 

It is also possible for short-term (< 1 day) fluctuations of humidity and wind speed to affect monthly latent heat flux estimates. We compared estimates made from 10-minute and monthly measurements (all using 10-minute scalar-averaged wind speed) and found mean biases of less than 3 W m^-2 at all locations. These results are similar to those of Esbensen and McPhaden (1996), which indicate that short-term correlations of scalar-averaged wind speed and humidity have very little impact on latent heat loss in the equatorial Pacific. However, we find seasonal variations to be more significant along 38°W, where ten-minute estimates are lower by ~ 10 W m^-2 during April and August-September at 8°N and during August at 12°N, with very little bias during the remainder of the year (generally less than 2 W m^-2 on a monthly basis). We therefore use 10-minute measurements of air temperature, SST, wind speed, and relative humidity to estimate latent heat flux. 

We obtained monthly climatological net longwave radiation from the da Silva et al. (1994) surface marine atlas. This parameter has an annual mean of close to 50 W m^-2 at all locations and varies less than ± 10 W m^-2 on a seasonal basis. 

Mixed layer depth estimates are affected by the development of shallow diurnal mixed layers. To avoid averaging these shallow effects into our estimates of mixed layer depth we use hourly SST, averaged between 5 and 7 a.m. local time, together with daily PIRATA subsurface temperature. We use linear interpolation to calculate the mixed layer depth as the depth at which temperature is 0.5 ºC below SST (Hayes et al., 1991). We then average these daily estimates to form a monthly mean cycle. This definition of mixed layer depth has the advantage that vertically averaged mixed layer temperature is very close to SST but has the disadvantage that vertical mixing at the base of the mixed layer may not be negligible. Errors in our mixed layer depth estimates result mainly from the 20 m vertical resolution of PIRATA subsurface temperature data. We estimate these errors by considering an idealized vertical temperature profile that is homogeneous within the mixed layer and linearly decreasing below. If we assume that the vertical gradient of temperature in the seasonal thermocline is ~ 0.1 °C m^-1 (typical of the tropical Atlantic, Levitus and Boyer, 1994), we find that our daily mixed layer depth estimates are too low by 0 to 5 m.

It is possible for surface freshwater fluxes to create salinity stratification within a deeper, nearly isothermal mixed layer (e.g., Ando and McPhaden, 1997). In such cases mixed layer depths based on temperature overestimate the true mixed layer depth. To assess whether this effect is important in the tropical Atlantic, we have compared mixed layer depth estimates based on vertical profiles of potential density (0.125 s_q criterion) to those with potential temperature (0.5 °C criterion) at each mooring location using the climatological (1°1°1-month resolution) data sets of Monterey and Levitus (1997). We find that, in the annual mean, mixed layer depth estimates based on temperature exceed those based on density by less than 6 m at each location. These differences are similar in magnitude, but opposite in sign, to the uncertainties associated with our estimates based on linear interpolation of vertical temperature profiles (discussed above). We therefore ignore both in our analysis.

To calculate horizontal temperature advection and vertical velocity we first estimate the seasonal cycle of near-surface horizontal velocity following the procedure of Grodsky and Carton (2001). This procedure combines more than 100 years of historical ship drifts, TOPEX/Poseidon sea level (1992 - 2001), ERS 1/2 surface winds (1992 - 2001), and velocity from hundreds of drifting buoys, deployed during 1997 - 2001 and drogued at a central depth of 15 m, to produce estimates with a 2°lat3°lon1-month resolution. The procedure uses optimal interpolation, with a first guess field consisting of long-term mean ship drift and drifter velocity, and applies corrections based on drifter/ship drift velocity and sea level. The analysis relies on simple assumptions such as geostrophy and Ekman balances off the equator and equatorial dynamics close to the equator. These velocity estimates are multiplied by 20-year (1982 - 2001) climatological monthly SST gradients (Reynolds and Smith, 1994) in order to estimate monthly horizontal mixed layer heat advection. We also use divergence of these velocity estimates, as well as estimates of the time derivative of mixed layer depth based on PIRATA subsurface temperature, to calculate w_e. Horizontal gradients of mixed layer depth are estimated from a monthly climatology based on bathythermograph temperature profiles (White, 1995).

We anticipate that meridional velocity in the mixed layer is primarily the result of Ekman drift (since the meridional component of geostrophic velocity is weak) that decreases with increasing depth. Our velocity estimates were calculated mainly from ship drifts, measured a few meters below the surface, and drifting buoys, with a 7 m drogue centered at a depth of 15 m. We thus expect that these values overestimate vertically averaged mixed layer meridional velocity under most circumstances, since the depth of the mixed layer remains greater than 15 m at all locations we consider. We therefore apply a correction that assumes a linear decrease in meridional velocity from the observed value at 15 m to zero at-h. No correction is applied for h < 15 m since we cannot accurately estimate surface velocity needed for interpolation from 15 m to the surface. This correction leads to annual mean mixed layer heat advection adjustments (with respect to values obtained from constant vertical profiles of meridional velocity) of less than 12 W m^-2 at all locations. On a monthly basis, adjustments are less than 20 W m^-2 at all locations, with the exception of 8°N, 38°W, where it is more than 30 W m^-2 during February as the result of a deep (~ 70 m) mixed layer. Since we cannot estimate the vertical distribution of zonal velocity, we have not applied a correction to zonal velocity estimates. 

It is known that tropical instability waves significantly heat the equatorial Atlantic mixed layer during boreal summer and fall through horizontal Reynolds heat fluxes. Since the typical period of tropical instability waves is less than one month, our climatolgical monthly heat advection estimates do not resolve them. Because in situ velocity measurements from the PIRATA buoys are not yet available, we are unable to estimate horizontal eddy advection directly. We therefore resort to the method of Baturin and Niiler (1997) and Swenson and Hansen (1999) to first calculate horizontal heat advection as the difference between the total and local time derivatives of mixed layer temperature:

The total time derivative is estimated from the SST measurements made by the (quasi-Lagrangian) drifting buoys, while the local derivative is estimated from climatological SST. We then subtract monthly climatological heat advection estimates (discussed previously) from (2) in order to estimate eddy heat advection. Estimates on the equator are uncertain due to poor spatial and temporal drifter coverage and the drifters? tendency to diverge from the equator. 

Since we are interested primarily in the seasonal cycle, we eliminate high-frequency variability by fitting the monthly averaged data to annual and semiannual harmonics using least squares (Fourier) analysis. We use the standard deviation from each harmonic fit as an estimate of the uncertainty associated with each term in (1). These error estimates account for high-frequency variability (period < 6 months) that our data cannot accurately reproduce. We also anticipate errors resulting from the combination of missing PIRATA data and interannual variability. In particular, it is possible for climatologies of different PIRATA variables to incorporate data from different time periods (see Fig. 2). For this reason we display the number of daily PIRATA measurements that go into each climatological monthly estimate at each location. Monthly estimates of each term in (1) use a maximum of about 120 individual daily measurements (since most PIRATA moorings have been operational for about four years). Low counts (<< 120) indicate high uncertainty.
 

3. Results

In this section we examine the balance of terms in (1) along two meridional sections in the west (38°W) and east (10°W) and a zonal section along the equator (see Fig. 1 for buoy locations). Examination of the mixed layer heat balance along 38ºW (Fig. 4) shows, as expected, that away from the equator surface heat flux balances local storage. Both absorbed shortwave radiation and latent heat loss terms have strong seasonal cycles at all mooring locations along 38ºW (see Table 1), and both are dominated by the annual harmonic. Absorbed solar radiation is highest in boreal spring, when the ITCZ is displaced to the south and the mixed layer is deep. Since surface shortwave radiation and mixed layer depth are very nearly in phase at 8ºN and 12ºN along 38ºW, the amplitude of absorbed shortwave radiation at these locations is even larger than that of surface shortwave (see Fig. 3).
 
 

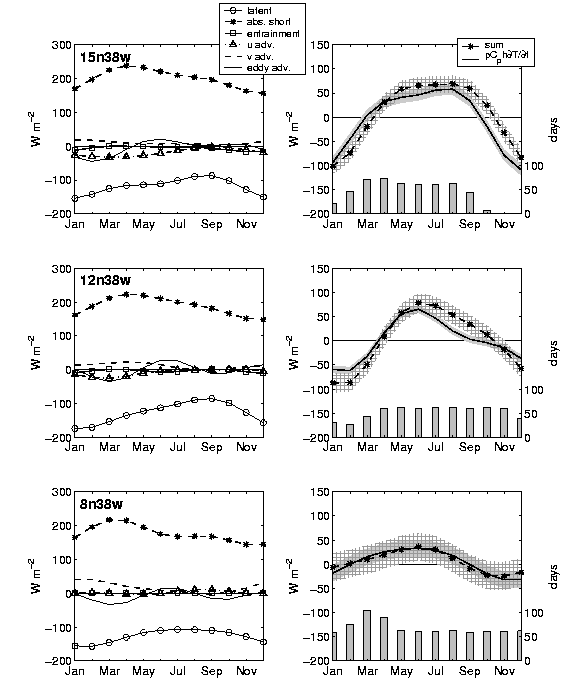Fig. 4. Left panels show individual contributions to the heat balance equation (1) in the form of latent heat flux, absorbed shortwave radiation, entrainment, mean zonal and meridional heat advection, and eddy heat advection (defined as total advection minus climatological monthly advection). Plots in lefthand panels show least squares fits of mean + annual and semiannual harmonics to monthly data. Righthand panels show the sum of the terms in the lefthand panel (plus longwave and sensible, which have been omitted from the lefthand panel) and the actual mixed layer heat storage rate. Shading and cross-hatching in righthand panels indicate error estimates based on standard deviations of monthly data from least squares harmonic fits. Bars in righthand panels indicate number of days in each month for which all PIRATA-based terms in the lefthand panel are available (maximum of ~ 120 days for each month, corresponding to ~ 4 years of data: September 1997 - February 2002).

 

Table 1. Amplitude and phase of annual and semiannual cosine harmonics (with respect to Jan. 1) and annual mean of terms in the mixed layer heat balance. Underlined terms are those that explain the largest amount of variance at each location. Units are W m^-2 for all terms except mixed layer depth, which is in meters.

 

	AnnualMean (W m-2)	Annual amplitude (W m-2)	Annual phase (months)	Semiannual amplitude (W m-2)	Semiannual phase (months)
15ºN 38ºW
Latent	-120	30	8	10	3
Surface shortwave	210	40	6	20	3
Absorbed shortwave	200	40	5	10	3
Entrainment	-10	10	5	0	3
Zonal advection	-20	20	9	0	3
Meridional advection	10	10	2	0	1
Eddy advection	-10	20	8	20	5
Heat storage	-10	80	6	30	3
Mixed layer depth	60 m	20 m	2	10 m	1
12ºN 38ºW
Latent	-130	40	8	10	4
Surface shortwave	210	30	6	10	3
Absorbed shortwave	190	30	5	10	3
Entrainment	0	0	7	10	3
Zonal advection	-10	10	9	0	6
Meridional advection	10	10	3	0	5
Eddy advection	0	10	8	20	0
Heat storage	0	50	7	20	5
Mixed layer depth	40 m	20 m	4	0 m	2
8ºN 38ºW
Latent	-130	30	8	10	5
Surface shortwave	200	20	4	20	3
Absorbed shortwave	180	30	4	20	3
Entrainment	0	0	7	0	4
Zonal advection	0	0	9	0	2
Meridional advection	20	20	2	10	1
Eddy advection	-10	10	8	20	0
Heat storage	0	30	6	0	2
Mixed layer depth	40 m	20 m	4	0 m	3

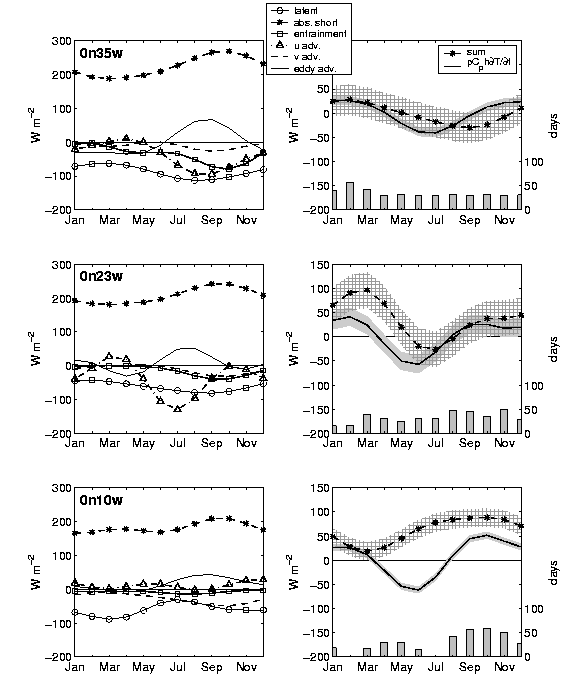Fig. 5. As in Fig. 4, but for locations along the equator.

Examination of the mixed layer heat budget at 0º, 35ºW reveals strong seasonal variations in zonal advection, with a period of maximum cooling in late boreal summer and weaker values during winter and spring. The phase and large amplitude of this term are explained by the fact that the zonal surface currents and temperature gradient vary in phase and are strongest during boreal summer when the equatorial cold tongue and the westward South Equatorial Current are well developed (see Fig. 1). Warming associated with horizontal eddy heat advection is also greatest during boreal summer and fall, when tropical instability waves are present in the western basin. The strength of the equatorial cold tongue and westward surface currents decrease throughout boreal fall and winter, resulting in decreased cooling by mean and eddy advection during this period. 

Absorbed shortwave radiation also has significant seasonal variability at 0º, 35ºW. The pronounced maximum in boreal fall coincides with clear skies and a deep mixed layer, while the minimum in spring results from cloudiness associated with the ITCZ and a shallow mixed layer. Despite a deep mixed layer in boreal fall, entrainment reaches a maximum during this period. Upward velocity at the base of the mixed layer at this time is supported by a decrease in the intensity of the westward South Equatorial Current in the eastern and central basin (resulting in an increase in zonal mass divergence) and a strengthening of the easterly trade winds (resulting in an increase in meridional mass divergence). As expected, latent heat loss undergoes weak seasonal changes at 35ºW associated with small variations in near-surface relative humidity.

The mixed layer heat balance at 0º, 23ºW shares many similarities with that at 35ºW. The maximum in zonal heat advection at 0º, 23ºW occurs in boreal summer (about a month earlier than at 35ºW) and is stronger than the corresponding maximum at 35ºW. This increased amplitude is explained by stronger westward surface currents and sharper zonal temperature gradients at 23ºW due to its position nearly midway between the center of the cold tongue to the east and warm SST to the west (see Fig. 1). Meridional heat advection cools the mixed layer at 23ºW during the second half of the year due to northward currents in the presence of a strong northward temperature gradient on the northern edge of the cold tongue.

Absorbed shortwave radiation at 23ºW varies with nearly the same phase as at 35ºW, but the annual mean and seasonal variations are smaller at 23ºW due to weaker annual mean and seasonal variations in mixed layer depth. Entrainment at 23ºW is also less significant than at 35ºW, although its seasonal cycle has nearly the same phase and is supported by similar mechanisms (meridional mass divergence resulting from easterly wind stress and zonal mass divergence resulting from a decrease in intensity of the South Equatorial Current in the eastern basin).

In contrast to the conditions at 0º, 23ºW and 0º, 35ºW, seasonal variations of zonal heat advection are insignificant along the equator at 10ºW. This location is near the center of the seasonal cold tongue (see Fig. 1) so that westward surface currents and temperature gradients are out of phase. The westward South Equatorial Current is strongest in boreal summer, when the cold tongue is well developed in the eastern basin and the zonal temperature gradient at 10ºW is small. The temperature gradient becomes increasingly negative throughout boreal summer and is strongest in October, when the cold tongue is weak and centered east of 10ºW. However, by this time zonal surface currents are weak near 10ºW and zonal heat advection remains small. In contrast, meridional temperature gradients are strong during the second half of the year at 10ºW when meridional velocity is ~ 10 cm s^-1. As a result, meridional heat advection cools the equatorial mixed layer significantly during boreal summer and fall.

Seasonal changes in shortwave radiation have a significant influence on mixed layer heat content at 10ºW. In contrast to the other equatorial locations, absorbed shortwave radiation at 10ºW has a significant semiannual harmonic, with a weak maximum in boreal spring and a stronger maximum in fall. The maximum in boreal fall results from simultaneous maxima in mixed layer depth and surface shortwave radiation and would be greater if not for the presence of reflective low-level clouds over the cool surface waters in early boreal fall. The weak maximum in boreal spring occurs when the mixed layer is shallow, but surface solar radiation is relatively strong since the ITCZ fails to reach all the way to the equator in the eastern basin.

In general, the agreement between the sum of forcing terms in (1) and the actual local heat storage rate is better off the equator along 38ºW than along the equator (Figs. 4 and 5). Along the equator, agreement is best at 35ºW, where zonal advection, entrainment, and latent heat loss tend to balance absorbed solar radiation and eddy heat advection. The agreement is worst at 10ºW, where the number of daily measurements is small for most months. The greatest residual in the heat balance at 10ºW occurs during June and July, when the sum of terms predicts warming of ~50 W m^-2 while the actual mixed layer heat content decreases by ~50 W m^-2. Explanations for this discrepancy include underestimates of entrainment, vertical turbulent diffusion, and latent heat loss. We first consider entrainment.

Our results along the equator suggest that entrainment is most important (in terms of both annual mean and seasonal variations) in the west. We find that entrainment cooling is more significant at 35ºW than in the central and eastern basin, where the mixed layer is significantly shallower. We anticipate that during boreal summer the easterly component of wind stress causes strong meridional divergence of mixed layer velocity ± ~ 2º from the equator. It is likely that our mixed layer velocity estimates (which have 2º meridional resolution) do not adequately resolve this process, resulting in entrainment estimates that are too low during boreal summer. Thus one possible explanation for the missing source of cooling at 10ºW is that we have underestimated meridional velocity divergence-induced entrainment. However, an average entrainment velocity of ~ 5 ´ 10^-3 cm s^-1 is required to explain the ~ 100 W m^-2 discrepancy during boreal summer at 10°W. This is nearly an order of magnitude larger than the maximum upwelling rate calculated by Weingartner and Weisberg (1991a) (0.6 ´ 10^-3 cm s^-1), averaged over eight months at 0º, 28ºW, and it suggests that entrainment alone cannot account for the additional cooling at 0º, 10ºW.

It is also possible that seasonal variations of vertical turbulent diffusion at the base of the mixed layer may alter mixed layer heat content at 0º, 10ºW. We have completely neglected this term since we do not have estimates of the turbulent exchange coefficient. Hayes et al. (1991) calculated this term explicitly in the eastern equatorial Pacific and found seasonal variations of up to 150 W m^-2 that were associated with changes in the vertical profiles of temperature and horizontal velocity.

An additional factor accounting for the discrepancy at 10ºW involves our estimates of latent heat loss. As discussed previously, data from only one year (2000) were used in the monthly latent heat flux estimates at this location. During this year relative humidity was anomalously high, leading to estimates of latent heat that are 50 W m^-2 lower than climatological estimates (da Silva et al., 1994). Such additional cooling could partially explain the discrepancy at 10ºW.

Our results at 0º, 35ºW and 0º, 23ºW along the equator generally agree with the results of Weingartner and Weisberg (1991b), who analyzed one year of upper ocean heat content data on the equator at 28ºW. They found a balance between meridional eddy advection, and vertical and zonal mean flow advection at 10 m. Their results indicate a period of cooling during mid-April through mid-May associated with upwelling-induced entrainment, followed by a period of warming mid-May through mid-July associated with enhanced meridional heat advection from tropical instability waves and cooling due to mean westward advection. At 23ºW and 35ºW we also find these terms to be important. During the remainder of the year they show that ocean dynamics do not contribute significantly to changes in SST and conclude that vertical diffusion must balance the net surface heat flux. In contrast, we find that entrainment is most important during the second half of the year. Interestingly, Carton and Zhou (1997) find that entrainment associated with meridional velocity divergence is an important source of cooling at these locations, while we find that zonal divergence is most important. The 25 W m^-2 excess cooling during boreal fall at 0º, 35ºW (Fig. 5) is likely due to an overestimate of zonal temperature advection, which likely overestimates the vertical scale of the South Equatorial Current.

In contrast to the conditions discussed above, south of the equator at 10ºW the mixed layer depth and surface shortwave radiation vary nearly out of phase. As a result, the amplitude of the seasonal cycle (annual + semiannual harmonics) of absorbed shortwave radiation at these locations is ~ 15 W m^-2 lower than that of surface shortwave. In contrast, latent heat loss has strong seasonal variations at 6ºS and 10ºS. Maximum latent heat loss occurs in boreal summer, when the southeast trade winds are strong and relative humidity is low.
 
 

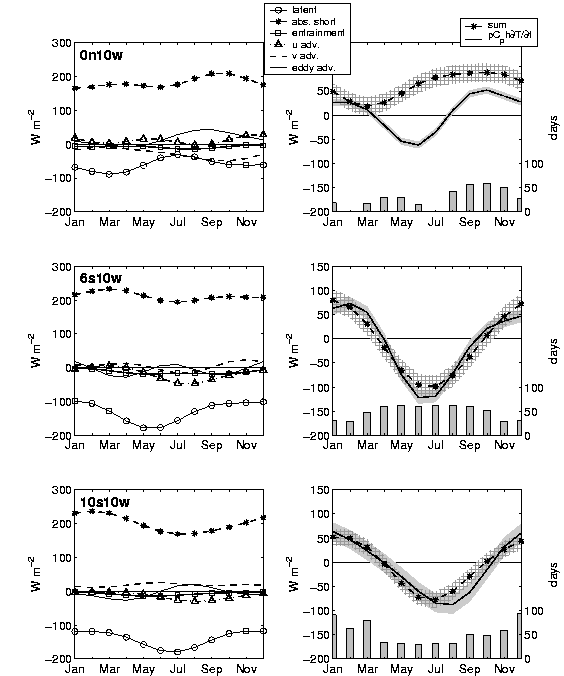Fig. 6. As in Fig. 4, but for locations along 10°W.

 

At these locations near-surface currents are from the northeast throughout the year. Zonal temperature advection is strongest during boreal summer, when the South Equatorial Current advects cool water westward. At 6ºS weak meridional advection provides cooling during boreal summer, when the equatorial cold tongue is well developed to the north, and heating during the remainder of the year, when the meridional temperature gradient is reversed. In contrast, at 10ºS the meridional temperature gradient is northward throughout the year, so that meridional advection provides a year-round source of heat. 

·In the eastern equatorial Atlantic (10ºW) cooling from meridional advection and warming from eddy advection tend to balance so that seasonal changes in SST tend to reflect seasonal variations in absorbed shortwave radiation. Entrainment and unresolved vertical diffusion may explain anomalous cooling, as discussed below.

DeWitt, D. G., and E. K. Schneider, The processes determining the annual cycle of equatorial sea surface temperature: A coupled general circulation model perspective, Mon. Weather Rev., 127, 381-395, 1999.

Enfield, D. B., Zonal and seasonal variations of the near-surface heat balance of the equatorial Pacific Ocean, J. Phys. Oceanogr., 16, 1038-1054, 1986.

Esbensen, S. K., and M. J. McPhaden, Enhancement of tropical ocean evaporation and sensible heat flux by atmospheric mesoscale systems, J. Clim., 9, 2307-2325, 1996.

Fairall, C.W., E.F. Bradley, D.P. Rogers, J.B. Edson, G.S. Young, Bulk parameterization of air-sea fluxes for TOGA COARE. J. Geophys. Res., 101, 3747-3764, 1996.

Freitag, H.P., Y. Feng, L.J. Mangum, M.P. McPhaden, J. Neander, and L.D. Stratton, Calibration procedures and instrumental accuracy estimates of TAO temperature, relative humidity and radiation measurements. NOAA Tech. Memo. ERL PMEL-104, 32 pp., 1994.

Freitag, H.P., M.E. McCarty, C. Nosse, R. Lukas, M.J. McPhaden, and M.F. Cronin, COARE Seacat data: Calibrations and quality control procedures. NOAA Tech. Memo. ERL PMEL-115, 89 pp., 1999.

Freitag, H.P., M. O'Haleck, G.C. Thomas, and M.J. McPhaden, Calibration procedures and instrumental accuracies for ATLAS wind measurements. NOAA. Tech. Memo. OAR PMEL-119, NOAA/Pacific Marine Environmental Laboratory, Seattle, Washington, 20 pp., 2001.

Grodsky, S. A., and J. A. Carton, Intense surface currents in the tropical Pacific during 1996- 1998, J. Geophys. Res., 106, 16673-16684, 2001.

Hansen, D. V., and C. A. Paul, Genesis and effects of long waves in the equatorial Pacific, J. Geophys. Res., 89, 10,431-10,440, 1984.

Hastenrath, S., Hemispheric asymmetry of oceanic heat budget in the equatorial Atlantic and eastern Pacific, Tellus, 29, 523-529, 1977.

Hayes, S. P., P. Chang, and M. J. McPhaden, Variability of the sea surface temperature in the eastern equatorial Pacific during 1986-1988, J. Geophys. Res., 96, 10553-10566, 1991.

Kalnay, E., et al., The NCEP/NCAR 40-year reanalysis project, Bull. Am. Meteorol. Soc., 77, 437-471, 1996.

Kessler, W. S., L. M. Rothstein, and D. Chen, The annual cycle of SST in the eastern tropical Pacific, diagnosed in an ocean GCM, J. Clim., 11, 777-799, 1998.

Klein, S. A., and D. L. Hartmann, The seasonal cycle of low stratiform clouds, J. Clim., 6, 1587-1606, 1993.

Koberle, C., and S. G. H. Philander, On the processes that control seasonal variations of sea surface temperatures in the tropical Pacific Ocean, Tellus, 46A, 481-496, 1994.

Lake, B. J., S. M. Noor, H. P. Freitag, and M. J. McPhaden, Calibration procedures and instrumental accuracy estimates for ATLAS air temperature and relative humidity measurements, NOAA Tech. Memo., in press, 2002.

Levitus, S., and T. P. Boyer, World Ocean Atlas 1994, Volume 4: Temperature. NOAA Atlas NESDIS 4, U.S. Department of Commerce, NOAA, NESDIS, 1994.

Medovaya, M., D. E. Waliser, R. A. Weller, and M. J. McPhaden, Assessing ocean buoy shortwave observations using clear-sky model calculations, J. Geophys. Res., 107, 3014, DOI 10.1029/2000JC000372, 2002.

Merle, J., Seasonal heat budget in the equatorial Atlantic Ocean, J. Phys. Oceanogr., 10, 464-469, 1980.

Moisan, J. R., and P. P. Niiler, The seasonal heat budget of the North Pacific: Net heat flux and heat storage rates (1950-1990), J. Phys. Oceanogr., 28, 401-421, 1998.

Molinari, R. L., J. F. Festa, and E. Marmolejo, Evolution of sea surface temperature in the tropical Atlantic Ocean during FGGE, 1979, 2. Oceanographic fields and heat balance of the mixed layer, J. Mar. Res., 43, 67-81, 1985.

Monterey, G. I., and S. Levitus, Seasonal variability of mixed layer depth for the world ocean, NOAA NESDIS Atlas 14, U. S. Gov. Printing Office, Wash., D.C., 5 pp., 87 figs., 1997.

Morel, A., Optical modeling of the upper ocean in relation to its biogenous matter content (case I waters), J. Geophys. Res., 93, 1652-1665, 1988.

Philander, S. G. H., D. Gu, D. Halpern, G. Lambert, N. C. Lau, T. Li, and R. C. Pacanowski, Why the ITCZ is mostly north of the equator, J. Clim., 9, 2958-2972, 1996.

Reynolds, R. W., and T. M. Smith, Improved global sea surface temperature analyses using optimum interpolation, J. Clim., 7, 929-948, 1994.

Richardson, P. L., and G. Reverdin, Seasonal cycle of velocity in the Atlantic North Equatorial Countercurrent as measured by surface drifters, current meters, and ship drifts, J. Geophys. Res., 92, 3691-3708, 1987.

Servain, J., A. J. Busalacchi, M J. McPhaden, A. D. Moura, G. Reverdin, M. Vianna, and S. E. Zebiak, A Pilot Research Moored Array in the Tropical Atlantic (PIRATA), Bull. Amer. Meteorol. Soc., 79, 2019-2031, 1998.

Stevenson, J. W., and P. P. Niiler, Upper ocean heat budget during the Hawaii-to-Tahiti shuttle experiment, J. Phys. Oceanogr., 13, 1894-1907, 1983.

Swenson, M. S., and D. V. Hansen, Tropical Pacific ocean mixed layer heat budget: The Pacific cold tongue, J. Phys. Oceanogr., 29, 69-81, 1999.

Wang, C. Z., and D. B. Enfield, The tropical Western Hemisphere warm pool, Geophys. Res. Lett., 28, 1635-1638, 2001.

Wang, W. M., and M. J. McPhaden, The surface-layer heat balance in the equatorial Pacific Ocean. Part I: Mean seasonal cycle, J. Phys. Oceanogr., 29, 1812-1831, 1999.

Weingartner, T. J., and R. H. Weisberg, On the annual cycle of equatorial upwelling in the central Atlantic Ocean, J. Phys. Oceanogr., 21, 68-82, 1991a.

Weingartner, T. J., and R. H. Weisberg, A description of the annual cycle in sea surface temperature and upper ocean heat in the equatorial Atlantic, J. Phys. Oceanogr., 21, 83-96, 1991b.

Weisberg, R. H., and T. J. Weingartner, Instability waves in the equatorial Atlantic Ocean, J. Phys. Oceanogr., 18, 1641-1657, 1988.

White, W. B., Design of a global observing system for gyre-scale upper ocean temperature variability, Progress in Oceanogr., 36, Pergamon, 169-217, 1995.

Wyrtki, K., An estimate of equatorial upwelling in the Pacific, J. Phys. Oceanogr., 11, 1205-1214, 1981.