Spherical Harmonic coefficients layout
The collection of Alm (spherical harmonics coefficient of degree l and order m) is stored in an array of complex double floating point values. The spherical harmonic truncation is defined by a call to shtns_init or to shtns_create which returns an shtns_cfg object (pointer to shtns_info) from which the the size of the array, shtns_info::nlm, can be read (see examples).
The field A is decomposed on the basis of spherical harmonics Ylm (degree l, order m) :
![\[ A(\theta,\phi) = \sum_{l,m} A_l^m Y_l^m(\theta,\phi)\]](form_8.png)
The series is truncated at degree LMAX and order MMAX*MRES, and only order that are multiple of MRES are described.
The NLM coefficients Alm are stored in a one-dimensional array, grouped by m.
The details of the storage may depend on the algorithm, and to access a particular coefficient, you should always use the following macros :
- LM(l,m) gives the index in the array for coefficient of degree l and order m.
- LiM(l,im) gives the index in the array for coefficient of degree l and order im*MRES.
Hence Alm[LM(l,m)] is the (complex) SH coefficient of degree l and order m.
- Note
- Since SHTns only deals with real spatial data, the Spherical Harmonic coefficients with negative m are related to the complex conjugate of the positive m coefficients :
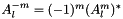 . For efficiency purposes, only the coefficients with positive m are stored.
. For efficiency purposes, only the coefficients with positive m are stored. -
There is no test on bounds, so that LM(l,m) with l or m that is not described, will give undefined result (in particular for an m that is not a multiple of
MRES)
To perform loops on all coefficients, use the macros LM_LOOP and LM_L_LOOP in combination of the arrays shtns_info::li which give the degree l and functions of it for any array index.
Allocation
Allocation for a SH description is simply done with :
The use of fftw_malloc ensures proper alignment of data for SSE vectorization (if fftw has been properly compiled with –enable-sse2 or –enable-avx).
Normalization
Several normalizations for the spherical harmonics exist (details on wikipedia). SHTns lets you choose one of the following :
-
Orthonormalized is the default (also used in the GSL)
![\[ Y_l^m(\theta, \phi) = \sqrt{\frac{2l+1}{4\pi}} \sqrt{\frac{(l-m)!}{(l+m)!}} \, P_l^m(\cos \theta) \, \exp(im\phi) \]](form_10.png)
-
Four-pi normalized
![\[ Y_l^m(\theta, \phi) = \sqrt{2l+1} \sqrt{\frac{(l-m)!}{(l+m)!}} \, P_l^m(\cos \theta) \, \exp(im\phi) \]](form_11.png)
-
Schmidt semi-normalized
![\[ Y_l^m(\theta, \phi) = \sqrt{\frac{(l-m)!}{(l+m)!}} \, P_l^m(\cos \theta) \, \exp(im\phi) \]](form_12.png)
shtns_init uses the default (defined by SHT_DEFAULT_NORM) but you can choose another normalization by calling shtns_create instead.
The Legendre associated functions are defined by :
![\[ P_l^m (x) = (-1)^m\ (1-x^2)^{m/2}\ \frac{d^m}{dx^m}P_l(x) \]](form_13.png)
which includes the Condon-Shortley phase 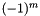 by default.
by default.
For reference, function SH_to_point gives a simple explicit implementation of the inverse SH transform (synthesis).
Normalization variations
Use shtns_create with SHT_NO_CS_PHASE to disable the Condon-Shortley phase. For example, to initialize a Schmidt semi-normalized transform of maximum degree 16 without Condon-Shortrley phase, use
By default, SHTns uses "complex" spherical harmonic normalization. However, as it deals only with real functions, the m<0 coefficients are not stored, since they are complex conjugate of the m>0 ones. Thus, one must pay attention, that the m>0 coefficient have to be counted twice in a total energy calculation.
An alternative to this "complex" normalization is the "real" normalization, for which the energy is simply the sum of the coefficients (m>=0) squared. Use shtns_create with SHT_REAL_NORM to use a "real" spherical harmonic normalization. This is the usual "real" spherical harmonics, if one takes the complex conjugate of the coefficients.
A few useful examples, for orthonormal spherical harmonics :
- a constant unit value on the sphere is represented by the coefficient
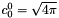 .
.  is represented by the coefficient
is represented by the coefficient 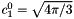 .
.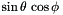 is represented by
is represented by 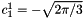 (with Condon-Shortley phase)
(with Condon-Shortley phase)- with a "real" normalization instead, one would have
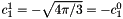 .
.
The functions sh00_1(), sh10_ct(), sh11_st() shlm_e1() will help to build simple spectral fields, no matter what normalization you choose.
Energy
- Note
- The energy of a scalar field can be retrieved from it's spherical harmonic representation as:
where![\[ \int ||q||^2 = \sum_{l,m \geq 0} C_m N_l \: |Q_l^m|^2 \]](form_21.png)
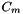 and
and 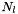 are the following normalization factor:
are the following normalization factor:- if SHT_REAL_NORM has been used,
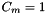 . Otherwise
. Otherwise 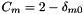 (ie
(ie 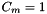 for
for 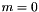 and
and 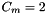 for
for 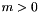 ).
). - for sht_orthonormal :
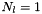
- for sht_fourpi :
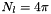
- for sht_schmidt :
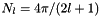
- if SHT_REAL_NORM has been used,
Troubleshooting
If you have problems in getting your spherical harmonic coefficient right, you may check the following :
- Schmidt semi-normalization ? try multiplying or dividing by
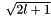
- Condon-Shortley phase ? try multiplying by
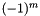
- Real or Complex ? try multiplying or dividing the m>0 coefficients by
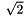
- Relative sign ? try to take the complex conjugate of the coefficients.
- Does the array include l=0 ?
 1.8.5
1.8.5