Before the end of the eighteenth century, most people believed that evaporation required the presence of air to dissolve the water. The term saturation vapor pressure arose because it was believed that this was the maximum amount of water vapor that could be dissolved in air. People erroneously believed that warmer air could dissolve more water vapor than cooler air. However, studies by De Luc and Dalton in the late eighteenth century cast doubt on these conclusions. The publication of Dalton's paper in 1802 finally resolved the issue. Dalton showed that the pressure of a gas is independent of the amount of other gases present. Because air is mostly empty space, each gas acts individually as if it alone existed. Most gases are indefinitely soluble in other gases (Ostwald 1891). In an equilibrium state, the amount of vapor above a liquid depends almost entirely on the temperature of the liquid. John Dalton concluded that the vapor pressure of water in air is independent of the existence of the air (Brutsaert 1991, Cardwell 1968, Greenaway 1966, Ostwald 1891, Dalton 1803).
Even today, many people believe that saturated air is holding as much water vapor as it can and that warm air holds more water vapor than cool air. Unfortunately, this mistaken belief has even made its way into some textbooks. A new general meteorology textbook (Nese et al. 1996) written by faculty members of The Pennsylvania State University should help to dispel this commonly held myth. In addition, a new atmospheric thermodynamics text by Bohren and Albrecht (1998) discusses this issue. A lucid non-mathematical explanation with illustrative examples is given by Bohren (1987).
Air does not hold water vapor. Water vapor is not dissolved in air. This can easily be demonstrated by a thought experiment. Imagine a closed container containing a beaker of pure water and a beaker of ocean water. Place the two solutions side by side so that they are at the same atmospheric temperature and pressure. The air above these two solutions is at the same temperature and pressure. If air "holds" water vapor, then the two solutions should have the same saturation vapor pressure. However, the saturation vapor pressure above the saline solution is less than that above the pure water. In the saline solution, the salt ions replace some of the water molecules so that fewer water molecules are available for evaporation (see Footnote 1). Therefore, the presence of the salt reduces the rate of evaporation from the saline solution compared to the solution of pure water. This then is the reason why the saturation vapor pressure above the saline solution is less than that above pure water. Note that the presence of initially identical air above the solutions could not account for this difference.
Saturation vapor pressure is actually something of a misnomer. The term saturation probably is an historical remnant from pre-Dalton times. It probably should be called equilibrium vapor pressure because, by definition, it is the water vapor pressure that occurs when a phase change is taking place. The higher the liquid water temperature, the more energetic are the liquid water molecules. The more energetic these molecules are, the more readily they can leave the liquid interface. This increases the amount of evaporation and therefore the saturation vapor pressure. The temperature of the air has nothing to do with it except that it can be eventually warmed or cooled depending on the temperature of the liquid surface. "Saturation" occurs when the evaporation rate equals the condensation rate and the air is in equilibrium with the liquid.
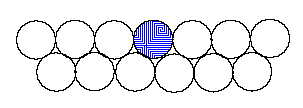
People commonly use relative humidity. As its name
implies, it is not an absolute measure of water vapor content. Relative
humidity is relative to saturation over a flat surface of pure water.
On a flat
surface, the forces on a water molecule from its nearest neighbors
tend to hold it in place and oppose the thermal energy of the molecule
tending to move it away. Notice that the dark circle has four nearest
neighbors.

When you have a curved surface such as a droplet,
each water molecule has fewer nearest neighbors than it would have on a
flat surface. In a cloud, these droplets can be as small as a
ten-thousandth of a micrometer and contain only a few dozen water
molecules. Notice that the dark circle in this figure has three nearest
neighbors.
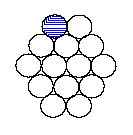
Of course, these figures are somewhat misleading because the molecules in the liquid water are three-dimensional and are moving in three dimensions. Therefore, consider these figures as a sort of average and perhaps this will help give you an idea of the situation. This effect of curvature on surface tension was discovered by Lord Kelvin. With fewer nearest neighbors, there is now less attractive force holding the water molecule to the surface. It is then easier for one of these water molecules to escape the intermolecular forces trying to keep it in the droplet. Because relative humidity is relative to a flat surface of pure water, the relative humidity of the air in equilibrium with this droplet can be much greater than 100%, depending on the curvature (i.e., size) of the droplet. This commonly occurs in clouds and has been called supersaturation. This is another unfortunate term because it is a thermodynamically stable state and there is nothing "super" about it. Only the conditions for equilibrium between the liquid and its vapor have changed. Like a flat surface, "saturation" above this droplet occurs when the rates of evaporation and condensation are equal and the air is in equilibrium with the liquid.
Despite this condition being referred to as supersaturation, the air actually has no difficulty accommodating this amount of water vapor. If you took a clean smooth container of pure water vapor, you could create a relative humidity of over 300% before you would get condensation. Fortunately, the real atmosphere has ubiquitous particles (e.g., salt, dust, etc.) that can act as condensation nuclei. Condensation nuclei act as solutes in the liquid cloud droplets. Solutes lower the equilibrium vapor pressure as mentioned above. The presence of a solute molecule at the liquid-vapor interface means that there are fewer water molecules available for evaporation. It is indeed fortunate for us that this occurs in the atmosphere. Otherwise, there would have to be a much larger quantity of water vapor in the atmosphere (it would have to become much more humid) in order to have rainfall (Rogers and Yau 1989). In the Earth's atmosphere, relative humidity rarely exceeds 101-102% within clouds. Outside of clouds and close to the Earth's surface, you can consider the relative humidity not to exceed 100%.
Key Points to Remember:
Footnote 1: Each sodium and chlorine ion actually is surrounded by a shell of water molecules held by strong ionic attraction between the ion and the polar water molecule. This attraction (hydration energy) is nearly as strong as that which the sodium and chlorine ions have for one another (this is why salt so readily dissolves in water). Therefore, the water molecules in this hydration shell are not as free to evaporate as those in a solution of pure water. The net effect is that there are fewer water molecules available for evaporation. This phenomenon is known as Raoult's Law (Adams, 1973).
Also, see Bad Meteorology by Professor Alistair Fraser.